CONSTRUCCIÓN DE POLIEDROS
SEMANA 32: Del 09 al 13 de noviembre
Elaboración del cubo infinito
Elaboración de un Teraedro con módulos de Snobe
Vivimos en una sociedad de cambios continuos en diferentes aspectos: en el trabajo, las relaciones sociales y hasta en el tiempo de descanso. Muchos ocupamos nuestro tiempo libre con nuestra lectura favorita, música favorita, funciones de cine en casa o algún juego de mesa, actividades que son posibles en el entorno del hogar y la familia. Ante la emergencia, las personas buscan elaborar planes seguros o reinventarse y tomar sus momentos de descanso como una oportunidad para la creatividad y aprender algo nuevo, como: la pintura, juegos como crucigramas, sudokus y algunos deportes acordes a las características, expectativas e interés de cada persona. Hemos buscado, en nuestro tiempo libre, elaborar juegos de una forma creativa, dinámica y recreativa, utilizado hojas de papel, cartulinas u otros materiales reutilizables que nos permitan construir formas geométricas bidimensionales y tridimensionales. Por ello, en la presente situación construiremos, con material reutilizable, formas geométricas tridimensionales como las pirámides y cubos, orientados al mejor uso del tiempo libre. Para comenzar, en esta actividad comprenderás las propiedades y características del cuadrado al construirlo para después elaborar el juego tridimensional.
CUADRADO:
Área del cuadrado de lado L = LxL
Área del cuadrado en función de la diagonal D = DxD/2
Perímetro de un cuadrado de lado L = 4L
TRIÁNGULO EQUILÁTERO:
Perímetro del triángulo equilátero de lado L= 3.L
PREGUNTA RETADORA
DIRECCIÓN DE TAREAS DE LA SEMANA 32:
2° A:
https://docs.google.com/forms/d/17GA0ChvrQ9HVkqgzIQyKNwacLQd0LmZ4mUpJyKK-o3k/edit
2° C:
https://docs.google.com/forms/d/1lGDw7E0iiNCmrRqoG7QVTCc1Fj9Z5veE5MC_PbnO2bU/edit


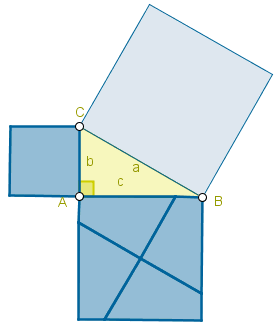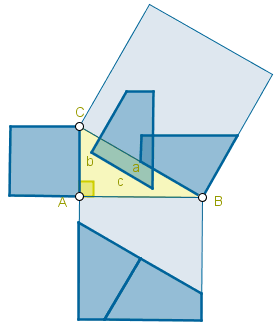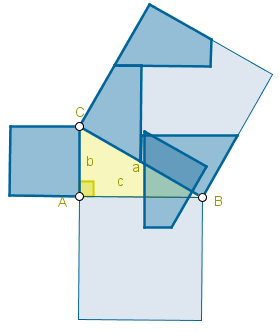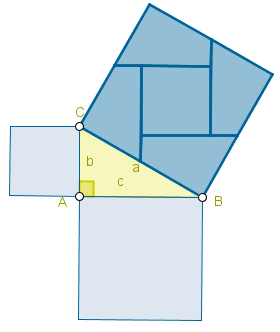




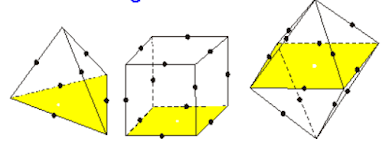
Buen día tengan todos hoy; planteamos la pregunta retadora de esta semana, espero sus intervenciones.
ResponderBorrarBuenas tardes profesor Fidel, soy Sebastian Tavara alumno del 2° grado "A". Con respecto a la pregunta retadora pasare a resolver la primera figura:
ResponderBorrarPrimero me fue muy dificil imaginar los puntos entrelazados, por esto recurri a la aplicacion Geogebra el cual pude concluir que se trataba de un octaedro:
V=√2/3*a³
Pero primero tenemos que saber cuanto vale la arista de la nueva figura, si los triangulos de tetraedro son equilateros, entonces los 4 triangulos internos que componen un lado del tetraedro tambien son equilateros, asi que solo dividimos el 10 entre 2 lo cual sera 5, ahora si podemos saber el volumen del octaedro:
V=√2/3*5³
V=0.4714*125
V=58,92557m³
Link de geogebra:(https://www.geogebra.org/classic?lang=es)
Gracias
Buen día Sebastián; tu esfuerzo es reconocido, muy bien
ResponderBorrarBuenas tardes profesor Fidel, disculpe la demora soy Mercedes Arce del 2do "C" y responderé a su actividad retadora:
ResponderBorrarCubo:
A= 10/2 = 5cm
V= 5^3 = 125cm3
Tetraedro:
A= 10/2 = 5cm Área de la base= b*h/2 = 5*5,590/2 = 13,98cm2
V= 1/3 * Ab * h
V= 1/3 * 13,98 * 5,590
V= 26,04 cm3
Octaedro:
A= 1072 = 5cm
V= a3√2/3
V= 5^3√2/3
V= 125*1.41/3
V= 176.8 /3
V= 58.92557cm3
Gracias y disculpe la demora.