CONSTRUCCIÓN DE FIGURAS POLIGONALES
SEMANA 31: Del 02 al 06 de noviembre
Elaboración de un cuadrado
Elaboración de un triángulo equilátero
Vivimos en una sociedad de cambios continuos en diferentes aspectos: en el trabajo, las relaciones sociales y hasta en el tiempo de descanso. Muchos ocupamos nuestro tiempo libre con nuestra lectura favorita, música favorita, funciones de cine en casa o algún juego de mesa, actividades que son posibles en el entorno del hogar y la familia. Ante la emergencia, las personas buscan elaborar planes seguros o reinventarse y tomar sus momentos de descanso como una oportunidad para la creatividad y aprender algo nuevo, como: la pintura, juegos como crucigramas, sudokus y algunos deportes acordes a las características, expectativas e interés de cada persona. Hemos buscado, en nuestro tiempo libre, elaborar juegos de una forma creativa, dinámica y recreativa, utilizado hojas de papel, cartulinas u otros materiales reutilizables que nos permitan construir formas geométricas bidimensionales y tridimensionales. Por ello, en la presente situación construiremos, con material reutilizable, formas geométricas tridimensionales como las pirámides y cubos, orientados al mejor uso del tiempo libre. Para comenzar, en esta actividad comprenderás las propiedades y características del cuadrado al construirlo para después elaborar el juego tridimensional.
CUADRADO:
Área del cuadrado de lado L = LxL
Área del cuadrado en función de la diagonal D = DxD/2
Perímetro de un cuadrado de lado L = 4L
TRIÁNGULO EQUILÁTERO:
Perímetro del triángulo equilátero de lado L= 3.L
PREGUNTA RETADORA
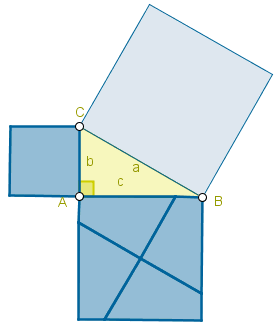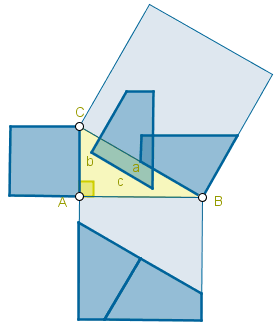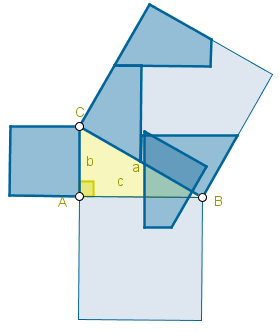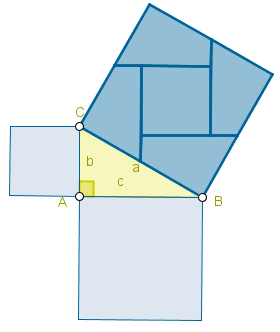
1) “Triángulo en cuadrado”
En el cuadrado ABDE se considera un punto C tal como indica la figura
¿Es ABC un triángulo equilátero?
DIRECCIÓN DE TAREAS DE LA SEMANA 31:
2° A:
https://docs.google.com/forms/d/11qHlAgINvJbf9M3J73nbJEjP4H3gMYfWFyhIBsHkv9c/edit
2° C:
https://docs.google.com/forms/d/1o-8T7R1fWQFR5MHqagW3Wv5SofBuSc3k_WGsW9Vt3JU/edit




Buen día a todos; planteamos la pregunta retadora de la semana; espero que participen con sus planteamientos y respuestas.
ResponderBorrarBuenas tardes profesor soy la alumna Jessica Ñiquen Silvestre del 2° "C"
ResponderBorrar1) “Triángulo en cuadrado”
¿Es ABC un triángulo equilátero?
Para contestar está pregunta voy a hallar la medida de los demás angulos de los triángulos:
Primero empiezo con el triángulo en dónde se muestra 2 datos
Teniendo en cuenta que al sumar los ángulos de cualquier triángulo siempre nos dar 180°
🔺EDC:
15° + 15° + x = 180°
______30° + x = 180°
____________X = 180° - 30°
____________X = 150°
Entonces decimos que:
El vértice "E" = 15°
El vértice "D" = 15°
E! Vértice "C" = 150°
🔺ECA:
Cómo se muestra en el vértice "E" se encuentran 2 ángulos separados pero en conjunto dan un ángulo recto, lo cual vendría a ser 90° y para hallar la medida del ángulo "x", el cual es el que no nos aparece que dato es, tenemos que :
15° + x = 90°
______x = 90° - 15°
______X = 75°
Y al suponer que el vértice "C" de este triángulo, vale lo mismo que el vértice "E", para hallar cual es el ángulo del vértice "A", debemos:
75° + 75° + x = 180°
_____150° + x = 180°
____________x = 180° - 150°
____________x = 30°
Entonces decimos que:
El vértice "E" = 75°
El vértice "C" = 75°
E! Vértice "A" = 30°
Y al suponer que el triángulo "ECA" vale lo mismo que el "CDB", Podemos ya plantearnos cuáles son los ángulos de triángulo "ABC" ya que podemos decir que:
El vértice "B" está dividido en 2 partes pero se sabe que en conjunto da un ángulo recto, lo cual equivale a 90° y para saber a cuánto equivale el ángulo "x" es decir el que debemos hallar en el vértice "B", debemos:
30° + x = 90°
______x = 90° - 30°
______X = 60°
Ya ahora que ya sabemos cuánto mide el ángulo del vértice "B" en este triángulo podemos decir que "B" y "A" valen 60° por ello para saber cuál es el ángulo de "C" debemos plantear está ecuación:
60° + 60° + x = 180°
_____120° + x = 180°
____________x = 180° - 120°
____________x = 60°
Entonces decimos que:
El vértice "A" = 60°
El vértice "B" = 60°
El Vértice "C" = 60°
R: Entonces podemos concluir que el triángulo"ABC" si es equilátero ya que los tres ángulos internos son iguales.
2) De todos los rectángulos de perímetro igual 36 metros, halle el rectángulo de máxima área.
Las alternativas son:
1 x 17 = 17
2 x 16 = 32
3 x 15 = 45
4 x 14 = 56
5 x 13 = 65
6 x 12 = 72
7 x 11 = 77
8 x 10 = 80
Y luego los números se repiten, por lo que tendríamos que elegir entre estás opciones y como se muestra, la respuesta sería 8 x 10, porque es el rectángulo con máxima área, ya que sale 80m^2, con un perímetro de 36m.
Muy bien la primer pregunta; en la segunda, ¿qué pasó con el 9x9?
Borrar´Buen día Jessica; la anterior pregunta equivale a decir que ¿todo cuadrado es un rectángulo?
BorrarBuenos días profesor. Soy Matias Torpoco Solano. Voy a responder la pregunta retadora de la semana.
ResponderBorrar1) “Triángulo en cuadrado”
En el cuadrado ABDE se considera un punto C tal como indica la figura
¿Es ABC un triángulo equilátero?
El triángulo ABC si es equilátero.
Demostración:
En el triángulo CDE, el ángulo C = 150 grados, por la medida de los ángulos internos de un triángulo.
En el triángulo ACE, el ángulo E = 75 grados, por sumar con el ángulo de 15 grados, 90 grados, ya que ambos forman un ángulo de 90 grados dentro del cuadrado ABDE.
El triángulo ACE y el triángulo BCD, son congruentes por LAL.
Entonces el lado AC, es igual al lado BC, dentro del triángulo ABC:
Podemos decir que : AC = BC
Si asumimos que el triángulo ABC es equilátero, entonces los ángulos alrededor del punto C, deberían ser 150, 60, 75 y 75, por sumar 360 grados por la propiedad de los ángulos alrededor de un punto.
De esta observación podemos afirmar que el triángulo BCD es isósceles por tener dos ángulos de 75 grados. Entonces, el lado BC es igual al lado BD.
En el cuadrado ABDE, el lado BD es igual al lado AB. Entonces, el lado BC es igual al lado AB.
Por lo tanto, podemos decir que:
AC = BC = AB
Entonces, podemos afirmar que el triángulo ABC es equilátero por tener sus tres lados iguales.
2) De todos los rectángulos de perímetro igual 36 metros, halle el rectángulo de máxima área.
En el rectángulo tenemos en el perímetro:
2a+2b = 36
2(a+b) = 36
a+b = 18
Si quiero obtener el área más grande, entonces las medidas de sus lados deben acercarse lo más posible. Por lo tanto:
a = 10 y b = 8.
Entonces el área más grande es igual a 10x8 = 80 metros cuadrados.
Buen día Matías; Muy bien la primer pregunta; en la segunda, ¿qué pasó con el 9x9?
BorrarBuenas tardes profesor. Soy Matías. El 9x9 no se considera porque, aunque sea el área más grande, representa el área de un cuadrado, y a nosotros nos piden el área más grande de un rectángulo.
BorrarBuenas tardes profesor Fidel soy Mercedes del 2do C y responderé las dos preguntas retadoras:
ResponderBorrar1.- ¿Es ABC un triángulo equilátero?
PROCEDIMIENTO:
El triángulo EDC tiene como tercer ángulo 160° ya que:
15° + 15° + x = 180
x = 180° - 30°
x = 150°
Por otro lado el triángulo AEC es congruente al triángulo CDB.
Para poder hallar los siguiente ángulos partiré el triángulo por la mitad para obtener dos triángulos rectángulos:
75° + 90° + a = 180°
165° + a = 180°
a = 180° - 165°
a = 15°
Ahora tenemos el valor de la mitad del ángulo A por lo que lo multiplicaremos por dos para hallar el verdadero:
x = 15° * 2
x = 30°
Ahora debemos hallar el ángulo restante del triángulo AEC:
75° + 30° + x = 180°
x = 180 - 165°
x = 75°
No olvidemos que los triángulos AEC y CDB son congruentes.
Por lo que si el ángulo A es 30° el ángulo B también lo es
30° + x = 90°
x = 60°
Ya tenemos dos ángulos del triángulo ABC por lo que el último ángulo se puede hallar de diversas formas:
FORMA N°1:
150° + 75° + 75° + x = 360°
x = 360° - 300°
x = 60°
FORMA N°2:
60° + 60° + x = 18°
X = 180° - 120°
X = 60°
RESPUESTA= El triángulo ABC es equilátero ya que sus ángulos internos son equivalentes y por lo tanto sus lados también lo son.
2.- De todos los rectángulos de perímetro igual 36 metros, halle el rectángulo de máxima área
Perímetro del rectángulo=
2b + 2h = 36
2 (b+h) = 36
b + h = 18
Nuestro objetivo es hallar la máxima área por lo que debe ser números que sean cercanos ( no puede ser 9 ya que se convertiría en un cuadrado) Entonces:
b = 10
h = 8
RESPUESTA= El rectángulo que tiene por base y altura; 10 y 8 es aquel con la máxima área.
Gracias y disculpe por la demora.
Buen día Mercedes; Muy bien la primer pregunta; en la segunda, ¿Qué pasó con el 9x9?
BorrarEste comentario ha sido eliminado por el autor.
BorrarBuenas tardes profesor Fidel, disculpe mi error.
BorrarHe investigado y en la geometría consideran que todos los cuadrados son rectángulos por lo que la respuesta sería un rectángulo de base y altura 9 cm.
Muchas gracias, disculpe la demora.
Buenos dias profesor Fidel, soy Sebastian Tavara alumno del 2° grado "A". Con respecto a la pregunta retadora:
ResponderBorrar1) “Triángulo en cuadrado”
En el cuadrado ABDE se considera un punto C tal como indica la figura
¿Es ABC un triángulo equilátero?
primero encontramos los angulos del triangulo de arriba, vemos que tiene 2 angulos de 15 grados, hacemos una pequeña ecuacion:
180=x+15+15
180=x+30
180-30=x
150=x
Ahora suponiendo que el angulo D(75°) del triangulo BCD es igual al angulo C del triangulo BCD se podria decir que el triangulo es equilatero ya que sus angulo son guales y como defecto sus lados tambien lo son.
2) De todos los rectángulos de perímetro igual 36 metros, halle el rectángulo de máxima área.
Perimetro:
2b+2h=36
2(b+h)=36
b+h=36/2
b+h=18
Entonces los lados no pueden ser de la misma medida ya que se convertiria en un cuadrado:
b=10
h=8
Gracias
Buen día Sebastián; Muy bien la primera pregunta; en la segunda, ¿Qué pasó con el 9x9?
BorrarBuenas noches profesor Fidel soy Claudio Ledesma del 2 "A":
ResponderBorrarPREGUNTA RETADORA
1) “Triángulo en cuadrado”
En el cuadrado ABDE se considera un punto C tal como indica la figura
¿Es ABC un triángulo equilátero?
Primero hallaría el ángulo C del triangulo superior.
Suponiendo que el triangulo superior tiene 15° grados seria.
180 = 15 + 15 + C
15 - 15 - 180 = C
150 = C
El Angulo C es 150
Suponiendo que el ángulo D y E son 75° ( por que los cuadros sus ángulos internos son 90° y eso lo restamos con los 15°) de los triángulos BCD y BCE se supone que el triangulo es equilátero ya que sus ángulo son iguales.
2) De todos los rectángulos de perímetro igual 36 metros, halle el rectángulo de máxima área.
Perímetro del rectángulo:
2b + 2a = 36
2(b + a) = 36
b + a = 18
Tenemos que hallar la máxima área por lo que debe ser números que sean cercanos.
b = 10
a = 8
Rpta.- El rectángulo que tiene por base y altura; 10 base y 8 altura es aquel con la máxima área 10 x 8 = 80.
Gracias.
Buen día Claudio; Muy bien la primer pregunta; en la segunda, ¿Qué pasó con el 9x9?
ResponderBorrarbuenas noches profesor soy piero lizana del 2"A"
ResponderBorrarBuenas noches profesor Fidel soy Claudio Ledesma del 2 "A":
PREGUNTA RETADORA
1) “Triángulo en cuadrado”
En el cuadrado ABDE se considera un punto C tal como indica la figura
¿Es ABC un triángulo equilátero?
El triángulo EDC tiene como tercer ángulo 160° ya que:
15° + 15° + x = 180
x = 180° - 30°
x = 150°
El vértice "E" = 15°
El vértice "D" = 15°
E! Vértice "C" = 150°
Entonces el lado AC, es igual al lado BC, dentro del triángulo ABC:
Podemos decir que : AC = BC
En el cuadrado ABDE, el lado BD es igual al lado AB. Entonces, el lado BC es igual al lado AB.
Por lo tanto, podemos decir que:
AC = BC = AB
entonces el triangulo ABC es equilátero por tener sus tres lados iguales.
2) De todos los rectángulos de perímetro igual 36 metros, halle el rectángulo de máxima área.
Perimetro:
Perímetro del rectángulo=
2b + 2h = 36
2 (b+h) = 36
b + h = 18
el objetivo es hallar la máxima área por lo que debe ser números que sean cercanos:
b = 10
a = 8
respuestas:el rectangulo que tiene por base y altura; 10 y 8 es aquel con la máxima área.
GRACIAS.